↓Skip to main content

[SIGMOD 2001] Orthogonal Optimization of Subqueries and Aggregation

·1327 words·7 mins
Paper Reading
Table of Contents

SQL 优化中，索引选择、Join Reorder、子查询优化是最难处理的几个问题。这是一篇 2001 年发表的经典论文，论文提出了 Apply、SegmentApply 算子和一批原子优化规则完成子查询去关联和相关优化。近期因为工作原因重温了这篇论文，我把我认为比较关键的一些内容整理出来，希望能帮助到各位朋友们。

子查询和常用执行策略 #

子查询提高了应用开发的灵活性，简化了用户写 SQL 的心智负担，在 SQL 的 scalar expression 中随处可见，比如下面出现在 WHERE 子句中的例子，查询每个客户的订单总额，找出总额大于 1M 的客户。

这样的子查询有很多执行策略，比如按照 SQL 描述的那样采用 correlated execution 的方式，读取一行 customer 的数据，替换子查询 where o_custkey = c_custkey 的 c_custkey 部分，然后执行子查询求每个客户的订单总和：

Q1

也可以采用先 outer join 再聚合的方式，先得到每个 customer 的所有订单，然后再按照 c_custkey 求每个客户的订单总额，等价的 SQL 如下：

Q1

还可以采用先聚合再 outer join 的方式，先对 orders 中的数据按照 o_custkey 聚合求出每个 customer 的订单总额，然后再和 customer 表 join 得到最终结果，等价的 SQL 如下：

Q1

哪种策略更好取决于很多因素，比如如果 customer 表数量不大，orders 表在 o_custkey 上有个索引，那么也许采用 correlated execution 的方式会更好。而如果 customer 表的数据量很大，每个 customer 的订单量也很多，那先聚合再 outer join 也许效果会更好，反之可能先 outer join 再聚合会更好。

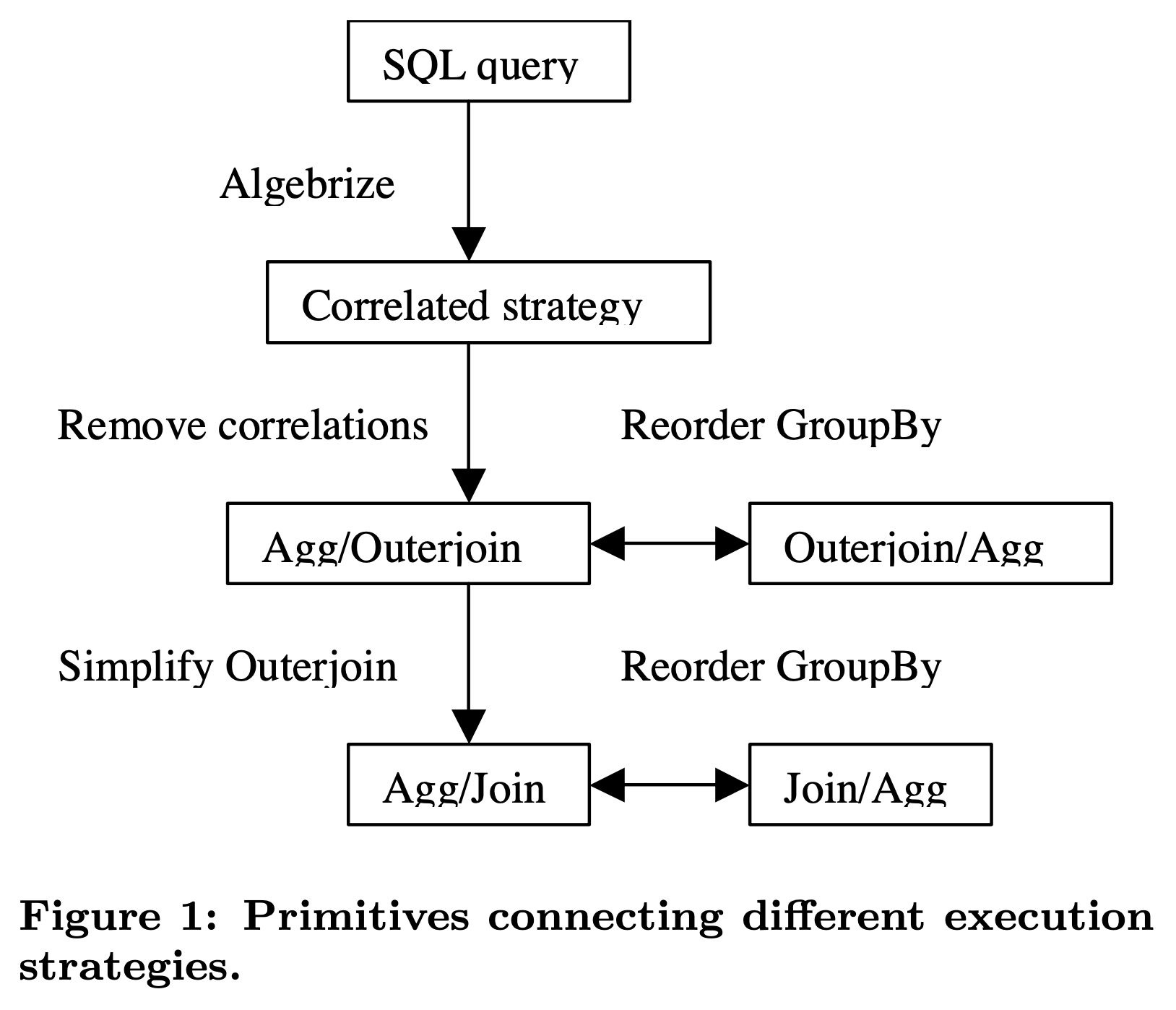
Primitives

如上图所示，这篇论文采用了原子的、正交的优化规则，结合 Volcano/Cascades 搜索框架同时枚举出这些可能的执行计划，再利用 CBO 选择最佳执行计划。为实现这一目的，需要先后经历这些过程：

  1. Algebrize into initial operator tree：将 AST 转换成 SQL 算子树，这里面利用 Apply 算子代表 correlated execution 策略，任意复杂的子查询都可以通过 Apply 来分解表示。
  2. Remove correlation：通过一系列的 Apply 下推和消除规则，完成关联子查询的去关联优化，消除 Apply 算子。
  3. Simplify outerjoin：Apply 消除后通常会产生许多 outer join，可以利用过滤条件的 null-rejection 属性将 outer join 转换成 inner join，进而可以触发其他优化规则，比如 join reorder。
  4. Reorder groupby：将 group by 操作下推到 join 之前，或者放到 join 之后执行，这样能够诞生出更多子查询执行策略，扩展 CBO 的优化空间。

我们先来看什么是 Apply 算子，再看看如何将 AST 中的子查询转换成 Apply。

Apply 算子的定义 #

论文在 1.3 小结给出了 Apply 算子的形式化定义，Apply 的语义启发自 LISP，可以简单看做一个 nested loop join：外层驱动表读取一行数据，执行内部的 subquery。和普通 Join 算子一样，Apply 连接左右两表的方式可以是 cross join、left outer join、left semi join、 left anti join 等，只要能产生满足 SQL 语义的正确结果就行。

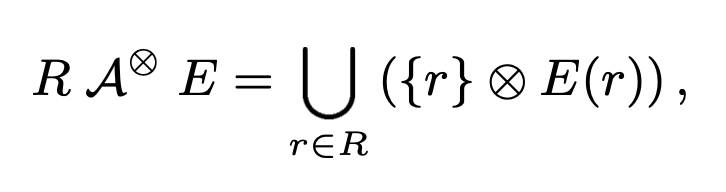
Apply

我们一开始提到的查询订单总额并过滤的 SQL：

Q1

它转换出来的 Apply 算子如下：

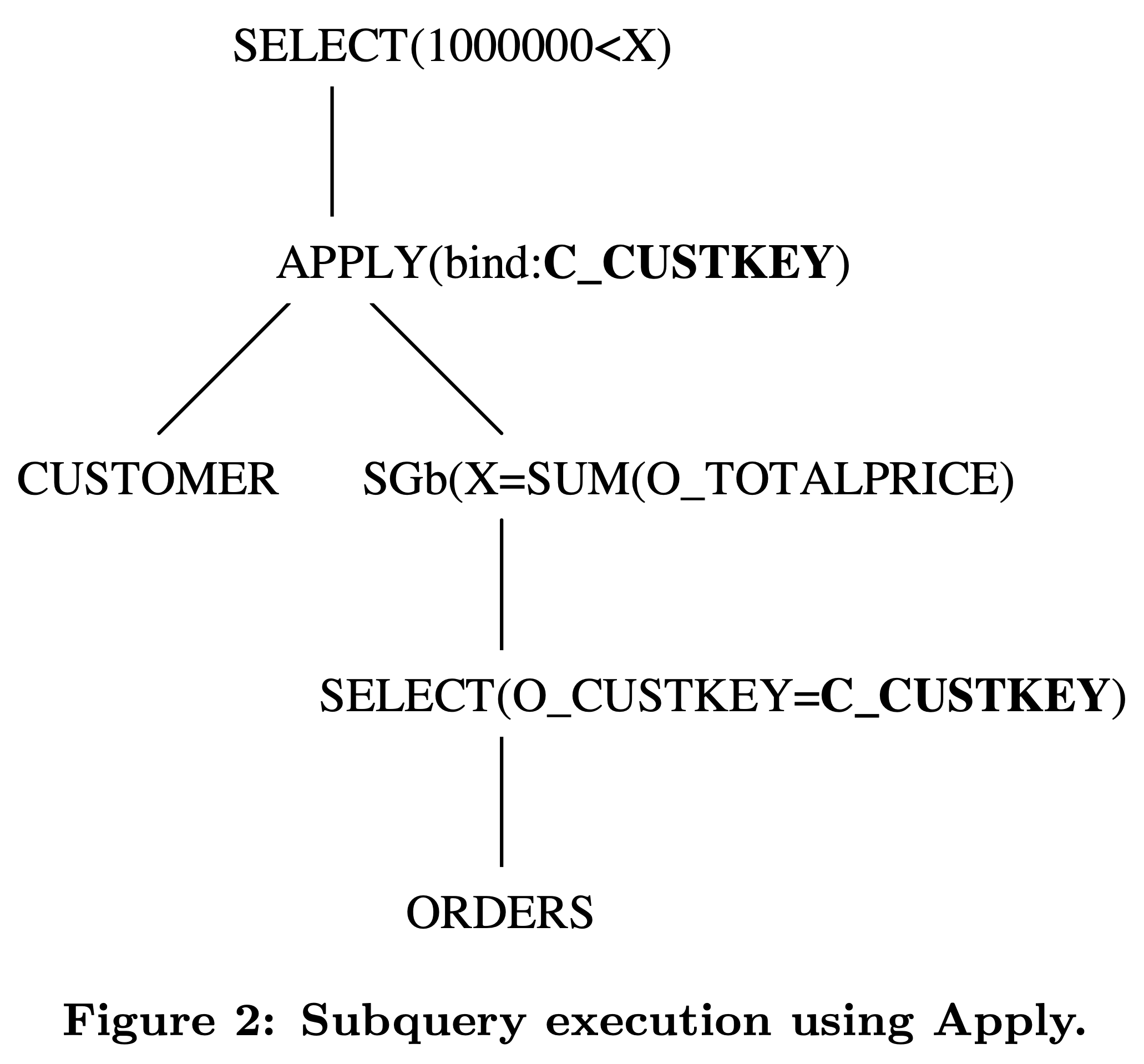
Subquery Execution Using Apply

如果 Apply 里面没有关联子查询，它其实等价于 nested loop join。Apply 算子的执行过程大致如下：

  1. 读取一行驱动表的数据，上面例子是 CUSTOMER 表。

  2. 根据该行驱动表的数据更新 Apply 算子所在子树的关联变量，上面例子中，假设读取上来的一行数据中 C_CUSTKEY 得值是 123，那么 O_CUSTKEY=C_CUSTKEY 绑定上这个运行时读上来的值后就变成了 O_CUSTKEY=123 这样的 filter。

  3. 执行 Apply 算子得到结果，返回给更上层的 SQL 算子。在上面的例子中，O_CUSTKEY=C_CUSTKEY 的 C_CUSTKEY 被更新后，Apply 算子为根的子 plan 就可以独立执行返回结果了。经过 SGb（scala group by，没有 group by key 仅返回一行结果的 group by 算子）得到一行数据，和外层 CUSTOMER 的这一行数据 join 后也仅产生一行数据，然后经过后续的 1000000<x 的过滤条件，完成后续计算。

了解了 Apply 算子的定义，那如何通过 Apply 算子进行子查询的优化和执行呢。要完成子查询优化，我们需要先将 AST 转换成 Apply 算子。

将 AST 改写成包含 Apply 的执行计划 #

AST

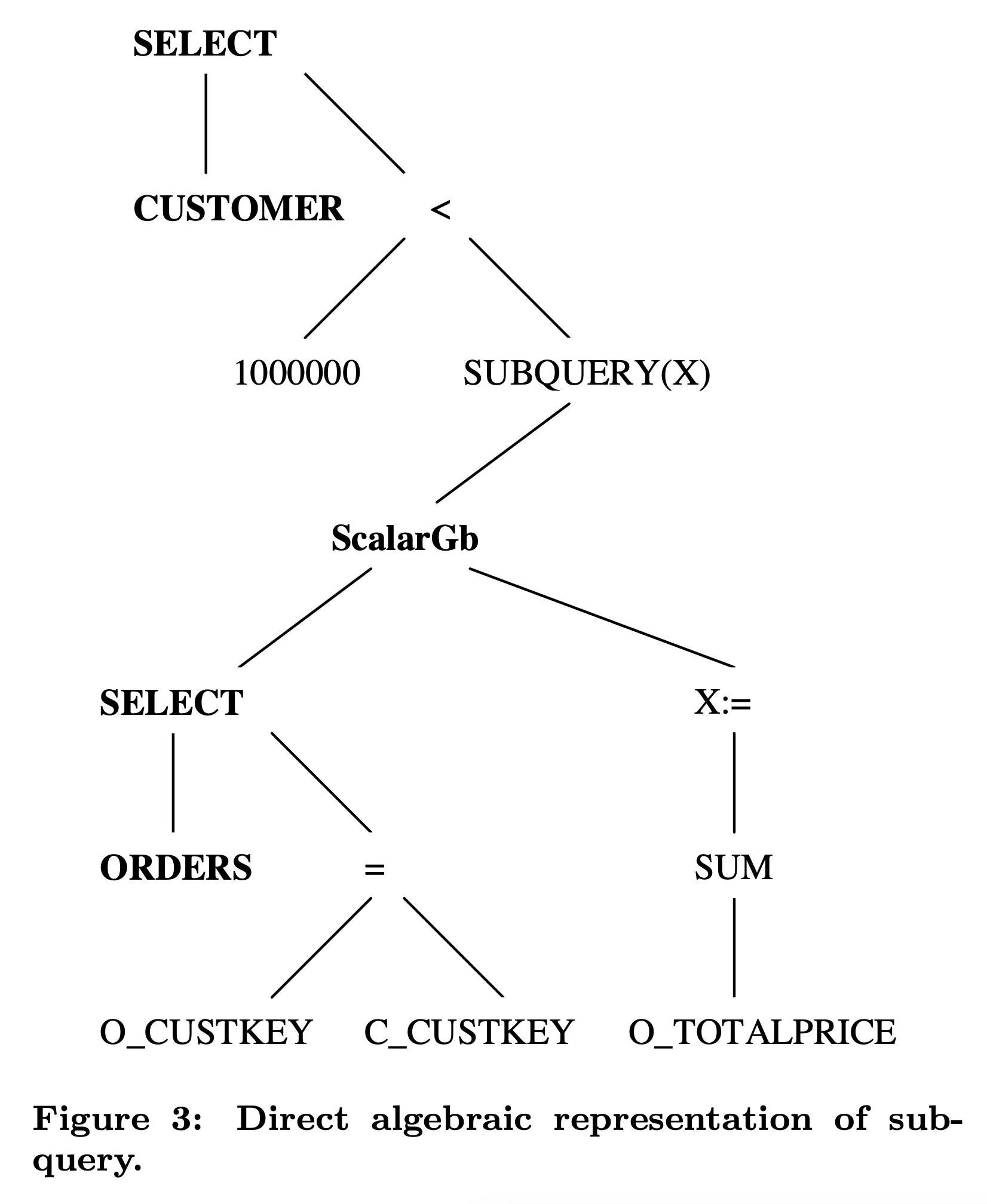
子查询通常出现在 scalar expression 中，比如上面例子，在构造 WHERE 子句的 SELECT 算子时发现一个 scalar expression 内嵌了一个 subquery，这个 subquery expression 里的 statement 描述了这个 subquery 代表的 scalar value 是如何计算出来的。

Apply 改写的基本思路比较简单，只需要在使用这个 Subquery 的 SQL 算子之前构造好为其提供 Subquery 结果的 Apply 算子即可。在上面这个例子中，我们需要在 SELECT 算子之前构造好 Apply，执行计划变成：CUSTOMER -> Apply -> SELECT，其中 CUSTOMER 作为 Apply 算子的左子树，而 Subuquery 里的语句构造出来的执行计划作为 Apply 的右子树，原先在 SELECT 中的子查询也需要替换成其他等价的 scalar expression，比如当 Apply 是 left outer join 时，IN subquery 就可以替换成对右孩子（代表子查询执行结果）某个字段的 IsNotNull 函数。

考虑到一方面子查询可能嵌套，另一方面一个 scalar expression 也可能包含多个子查询，而且我们在改写完子查询后还需要替换成新的 scalar expression，因此最好采用 bottom up 的方式递归构造子查询对应的 Apply 算子和新的用于替代当前它的新的 scalar expression：

  1. bottom up 的遍历 scalar expression 树，如果发现 child expression 已经被改写了，就更新其 child 信息

  2. 遍历自己，如果需要进行子查询改写，则根据子查询的类型生成相应的 Apply 算子和改写后的 scalar expression。构造 Apply 时将当前 scalar expression 所在 SQL 算子的孩子节点作为新 Apply 算子的左孩子，子查询对应的执行计划作为新 Apply 算子的右孩子，根据 subquery 的语义选择适当的 join 类型（left outer join、cross join 等）。新的 scalar expression 使用构造出来的 Apply 算子的结果做为输入。

通过这样 bottom up 的遍历后，我们就得到了最终的 Apply 算子和需要替换的 scalar expression，然后继续遍历 AST 的其他部分，构造剩余的 query plan，完成从 AST 到执行计划的转化。

因为整个过程是递归的，每个子查询都会遍历到并转换成相应的 Apply 算子和 scalar expression，当这种方法应用到包含多个子查询的场景时，最终会生成一棵类似下面这样的 Apply 左深树：

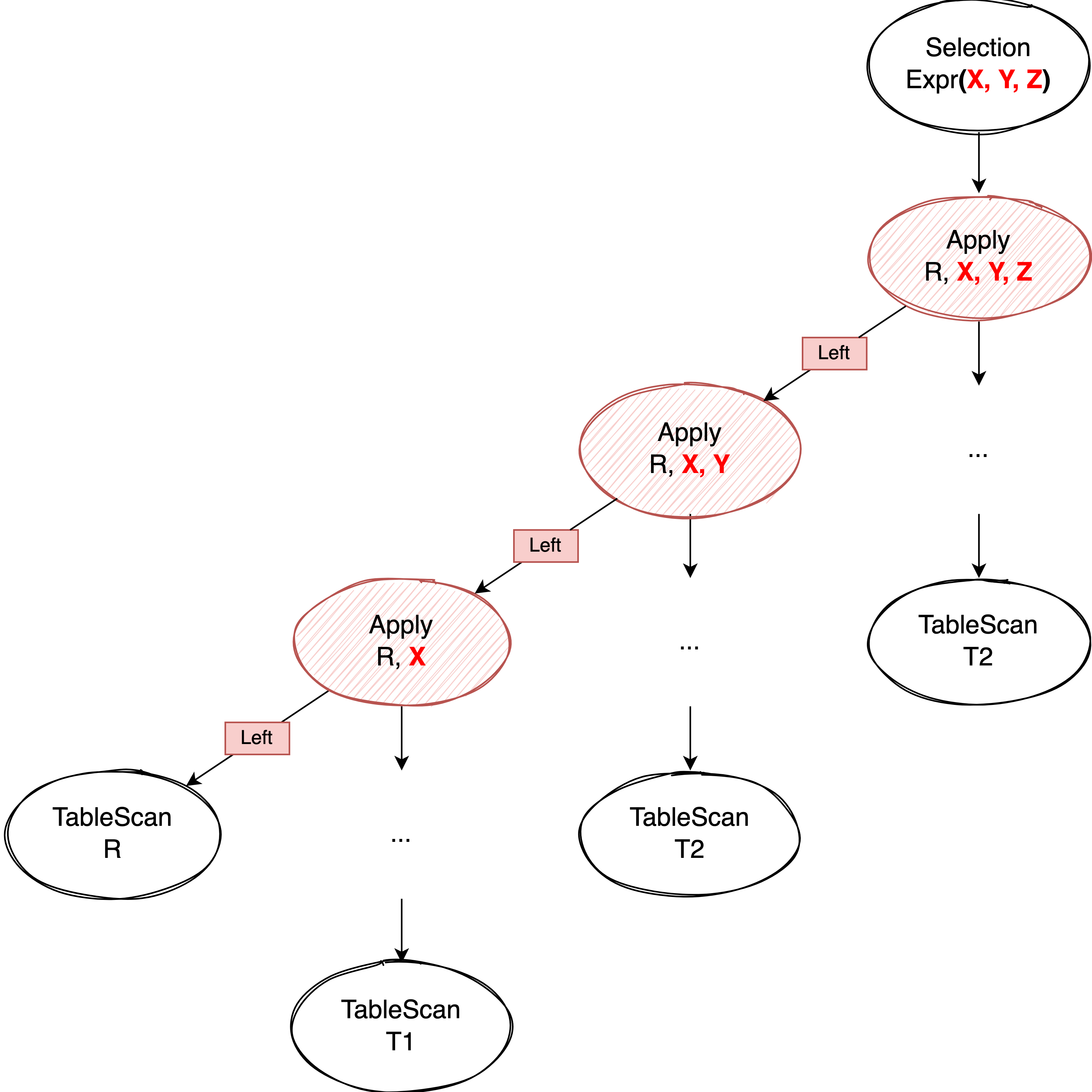
Left Deep Tree

IN、NOT IN 的改写 #

IN 可以改写成 Distinct + Apply：先通过 Apply 计算出 left outer join 的结果，然后将 Selection 中的子查询改为 Apply 产生的右表 column 的 IsNotNull 即可，如果是 NOT IN 就改写成 IsNull。

比如 where t.id in (select id from s) 就改写成了：

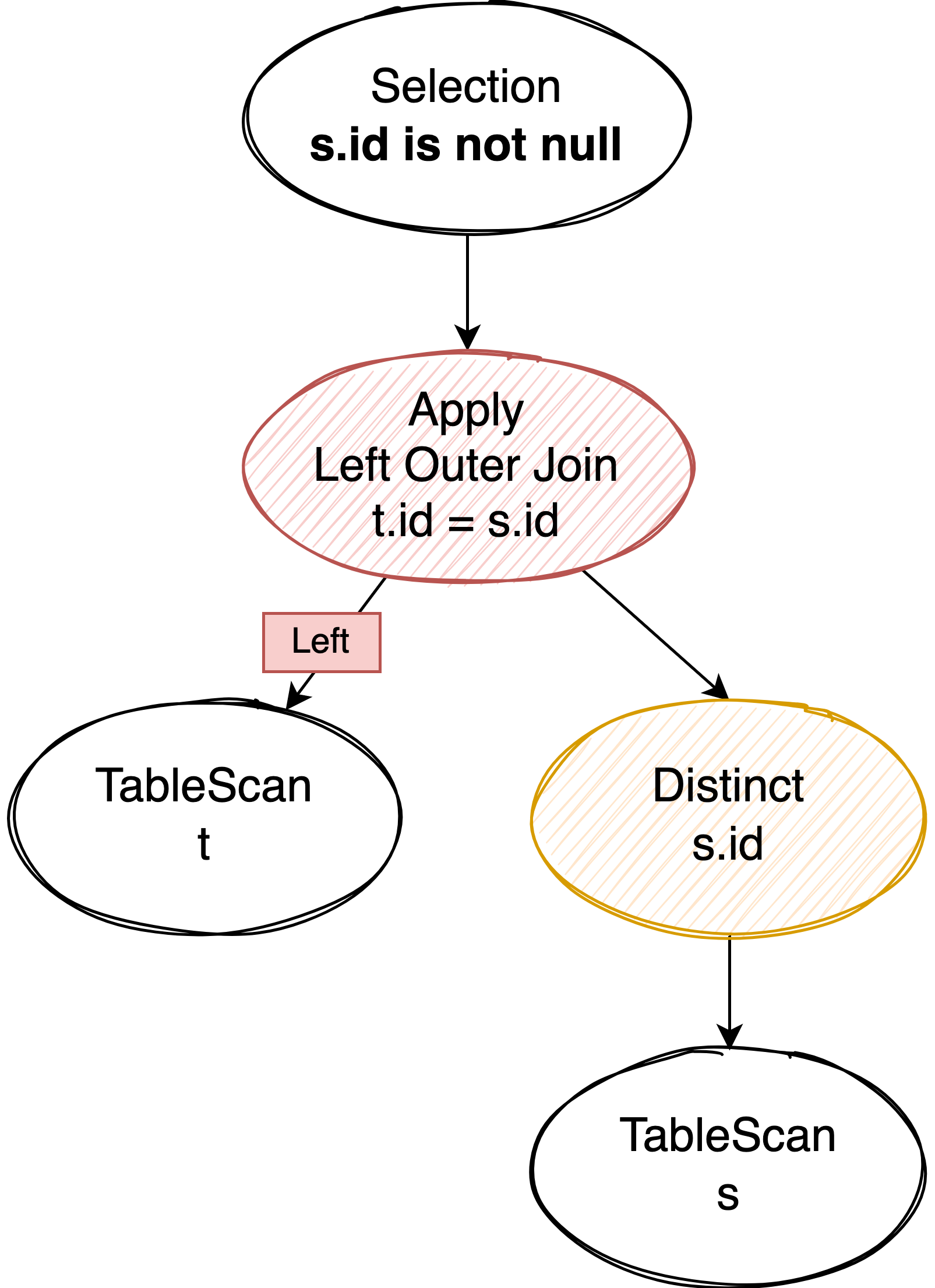
In Sub-Query

对子查询的结果加 Distinct 去重是为了确保驱动表的数据经过 left outer join 后不会发生膨胀，如果能 join 上则只会有一条数据产生，如果没有 join 上则会把右表部分填补成 NULL 后也产生一条结果。因此 Apply 的输出结果里有完整的左表数据，我们也能根据输出结果中右表部分的数据是否为 NULL 来判断是否 join 上（也就是 IN 子查询的结果应该是 true 还是 false）。

EXISTS、NOT EXISTS 的改写 #

和上面 IN、NOT IN 大致相同。

compare predicate 的改写 #

保留原本的 compare operator，把相关的 parameter 用子查询的结果替换。子查询根据需要改写成 Aggregate 或者 MaxOneRow（新算子，用于确保用户没有写 group by 但是又要求结果只产生一行数据的情况）。

Apply 的下推和消除 #

Appy 算子本身是可以执行的，但通常如果内表没有索引，或者外表的数据量非常大，Apply 的执行效率会非常低，为了搜索可能更优的执行计划，需要进行 Apply 相关的优化，将 Apply 转换成没有关联子查询的普通 Join，然后利用 Join 相关的优化规则搜索可能更优的执行计划。

下面是论文给出的所有 Apply 消除会用到的原子优化规则。SQL Server 采用了 Volcano/Cascades 优化框架，每个优化规则只需要匹配一个 Plan 片段即可，因此 Apply 下推直至消除所需使用的优化规则都可以一遍遍的应用到新产生的执行计划中，直至优化结束：

Rules

这些公式看起来复杂，但理解起来不难，可以把他们分为 2 类：一类是直接消除 Apply 算子的，可以认为是 Apply 消除算法的终止条件，另一类就是不断进行 Apply 下推寻找 Apply 消除机会的，我们分别来介绍他们。

规则 1 - 2：Apply 消除 #

规则 1：当 Apply 的左表和右表没有任何 join 条件时，不管这是个什么 join（cross join、left outer join, left semi join、left anti join），都可以将 Apply 转换成普通 Join 算子。

规则 2：对 Apply 而言，右孩子的 Filter 可以等价转换成 Apply 的 join 条件，完成这次转换后，Apply 就和普通 nested loop join 没有什么区别了，可以安全的将其转换成普通 Join 算子。

需要注意的是：

  1. 规则 1 和 2 能够生效的公共条件是 Apply 的右孩子中，E 代表的执行计划不包含 R 的相关列。
  2. 理论上来说 Apply 转换后的执行计划不一定什么情况下都更好，比如当左表的数据量很小，右表在相关联列上有索引，或者右表已经提前物化到了计算节点上时，可能 Apply 算子这种 nested loop 的执行方式会更好，之前在一些客户场景中遇见过这样的情况。保险的做法是把 Apply 算子代表的老执行计划也留下来，通过 CBO 来选择。怎么样让 CBO 选择更准确就是另一个问题了。

规则 3 - 9：Apply 下推，寻找消除的机会 #

规则 1 和 2 描述了 Apply 消除的终止条件，而规则 3-9 则描述了在各个场景下 Apply 如何下推，行成可以触发规则 1 和 2 的执行计划。

  1. 规则 3 和 4 分别描述了 Apply 下推过 selection 和 pojection 的场景。
  2. 规则 5 和和 6 分别描述了 Apply 下推过 union [all] 和 intersect [all] 的场景
  3. 规则 7 描述了 Apply 下推过 cross join 的场景，需要注意的是：
    1. 下推后 R 表在左右两个 Apply 算子中分别被读了 1 次，如果底层没有采用 DAG 的 execution model 使得 R 表可以只读一次被多个 parent 复用可能会有很大的性能损耗，使得下推后的 Apply 不如下推前执行效率好。
    2. 下推后取代原始 Apply 的是一个 inner join，为了确保 R 表的每行数据仍然只会产生一行结果，这个 inner join 的 equal condition 需要在 R 表的某个唯一索引、主键或者其他可以唯一决定一行数据的字段上（比如 row id）。
  4. 规则 8-9 分别描述了 Apply 下推过 vector aggregation 和 scalar aggregation 的场景。
    1. 因为下推过 Aggregation 后要确保 R 的每行数据只产生一行结果，我们需要保证新产生的 Aggregation 的 group by key 也是某个能唯一确定 R 表一行数据的主键、唯一索引、或者类似 row id 一样的字段。
    2. 另外对于规则 9 来说，先后的 aggregation 分别是 scalar aggregation 和 vector aggregation，需要特别注意某些聚合函数对 empty set input 和 null input 的结果差异。

Apply 下推和消除的例子 #

Example

与 Aggregate 相关的所有优化规则 #

在子查询改写成 Apply 算子，以及 Apply 算子下推、消除的过程中，会诞生 Aggregate 和 Join 算子，因此扩大了搜索空间，诞生了更多优化的可能。

论文的 3 小结 “COMPREHENSIVE OF AGGREGATION” 详细介绍了 Aggregate 相关的优化。其中一些聚合相关的优化在另一篇比较早期的经典论文《 Eager aggregation and lazy aggregation》中也提到了，感兴趣的朋友可以去看看。

Reordering Aggregate Around Filter #

为啥是 reorder 不是单纯的 pull up 或者 push down，主要原因还是这两种策略都有各自的最佳场景。reorder 的目的是枚举出所有这些可能的执行计划，把选择交给 CBO 的代价模型去评估。

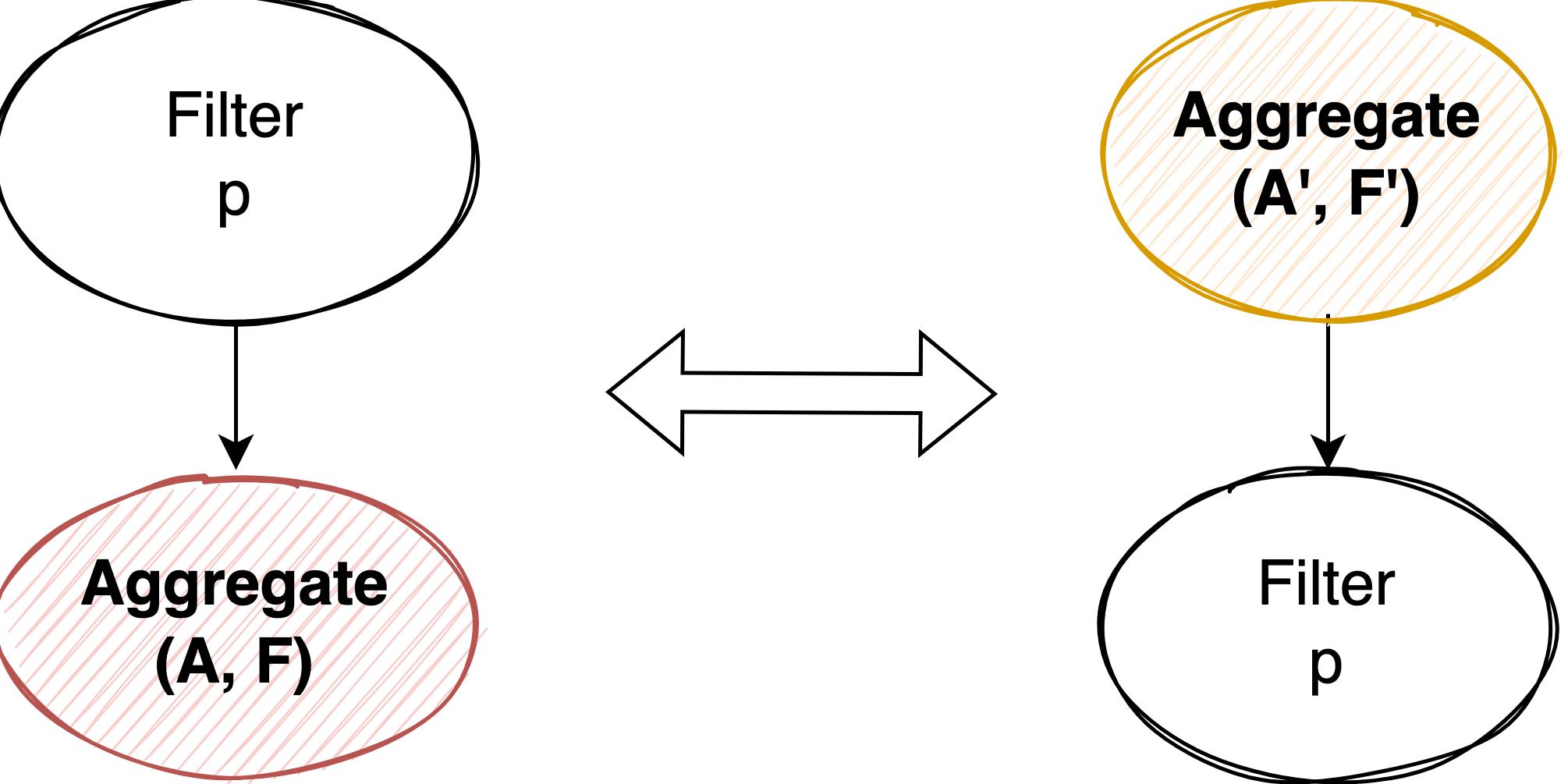
GroupBy Around Filter

we can move a filter around a GroupBy if and only if all the columns used in the filter are functionally determined by the group- ing columns in the input relation.

这个比较好理解，当且仅当 Filter 是对整个 group 过滤时才能将 Aggregate push down 或者将 Aggregate 从 Filter 下面 pull up。判断 function dependency 的简单方法是检测 Filter 使用的 column set 是否是 Aggregate 中 group by 的 column set 的子集。

Reordering GroupBy Around Join #

GroupBy Around Join

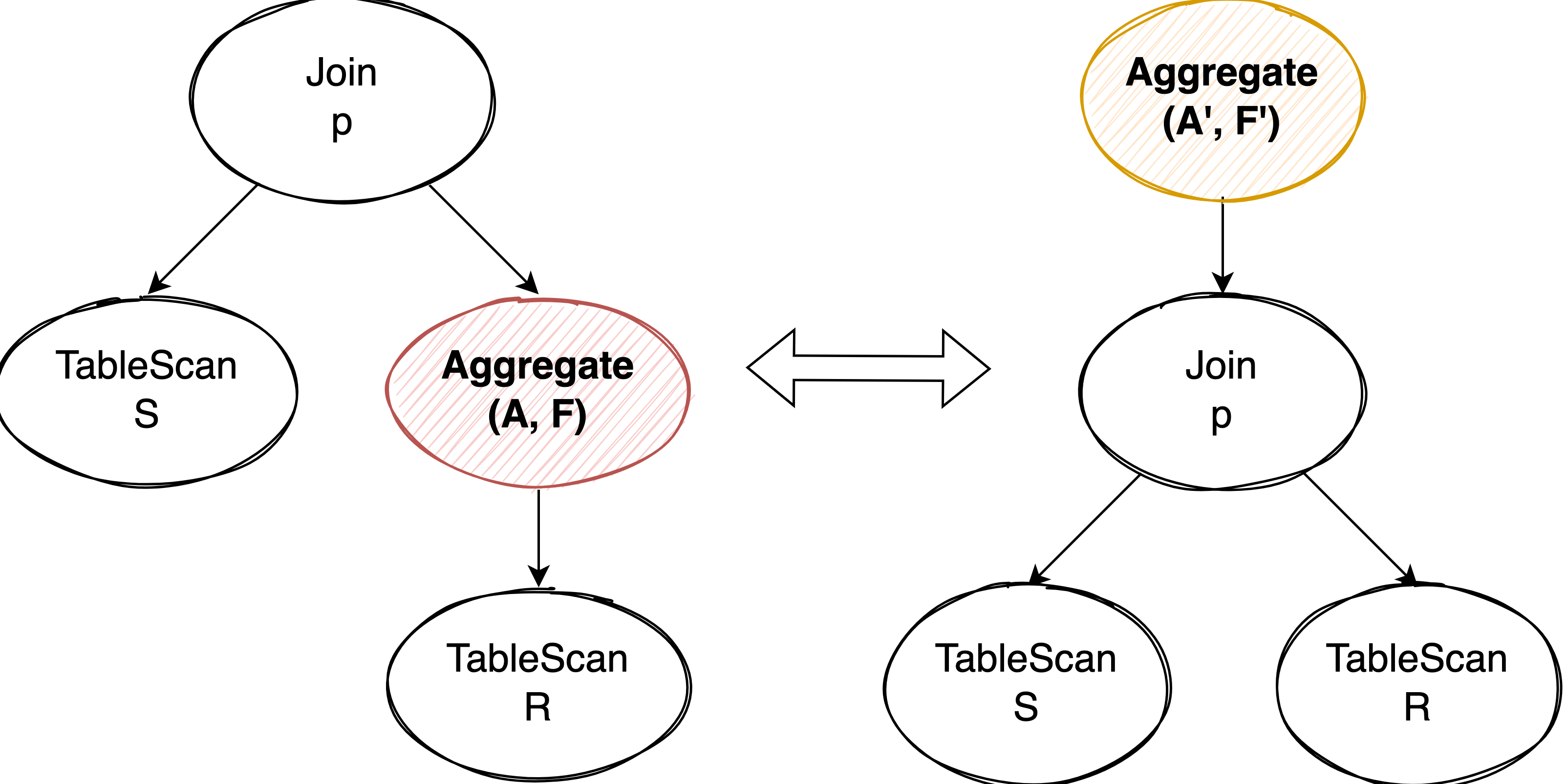
那什么情况下 Aggregate 可以完全的 push down 或 pull up 过 Join 算子呢。我们以 Aggregate pull up 为例：

  1. Join 可以看做是先 Cross Join 再 Filter，因此要想使 Aggregate 能够 pull up 或 push down Join，也要求 Join Condition 使用的 column set 是 Aggregate 中 group by 的 column set 子集，满足 functional dependency。
  2. 左右两个执行计划的结果集大小需要保持一致。对于左边的执行计划来说，结果集的大小取决于 S 表的数据量和每一行 S 表数据能 join 上多少行 Aggregate 后的结果。这意味着 Aggregate pull up 后需要按照 S 表的某个主键或唯一索引以及原来的 R 表上的 group by 字段进行分组。
  3. 还有一点在 push down 时需要满足的条件：Aggregate 中聚合函数使用的 column set 必须全部来自 R 表，这样才能顺利将 Aggregate push 到 R 表上面。

因为 Join 看做是 Cross Join 后再 Filter，在 Aggregate pull up 或 push down 的时候，如果发现不满足条件的 join condition，我们可以单独抽取一个 Filter 出来计算这些 condition 使得 join condition 满足条件 1。

对于 left semi join 或 left anti semi join，他们也可以看做是先 join 再 filter，因此 Aggregate push down 或 pull up 可以采用同样的方式。

Reordering GroupBy Around Outer Join #

GroupBy Around Outer Join

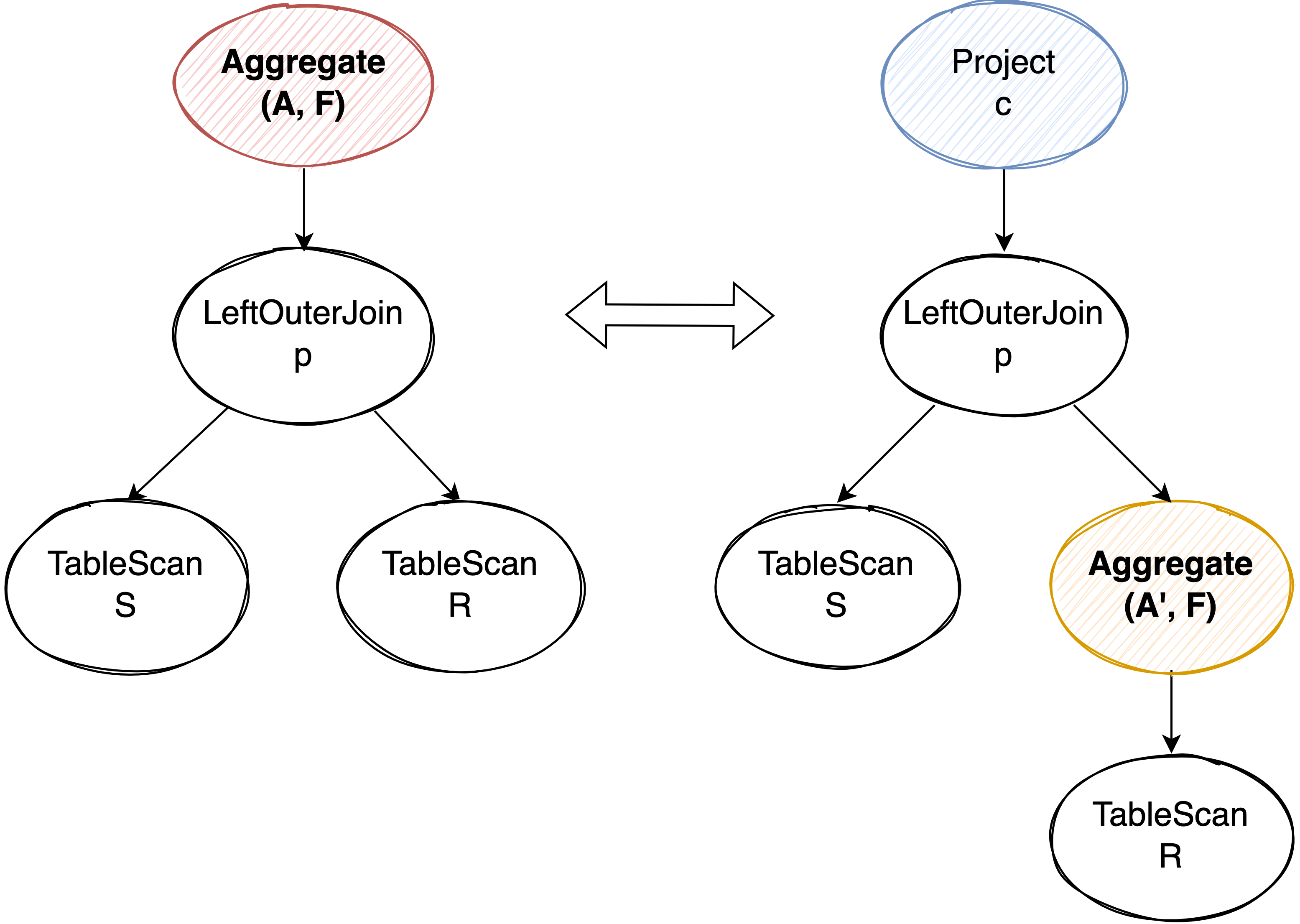
push down Aggregate 到 outer join 下面会稍微特殊一些。对于 outer join 来说，没有 match 上的数据会用 NULL 来填补，之后聚合函数对 NULL 值进行计算。需要注意的是，虽然大多数聚合函数（比如 sum）在输入是 NULL 时输出也是 NULL，但也有特殊情况，比如 count(*)，在输入为 NULL 的时候输出为 0。

如果我们直接把 Aggregate 下推到右表上，没有 join 上的数据会输出 NULL，就和左边的执行计划在计算 count(*) 时输出 0 结果不一致了。因此我们在聚合下推后需要在原来 outer join 上面补充一个 Project 算子，用来模拟 NULL input 时各个聚合函数应该输出的结果。

Local Aggregate #

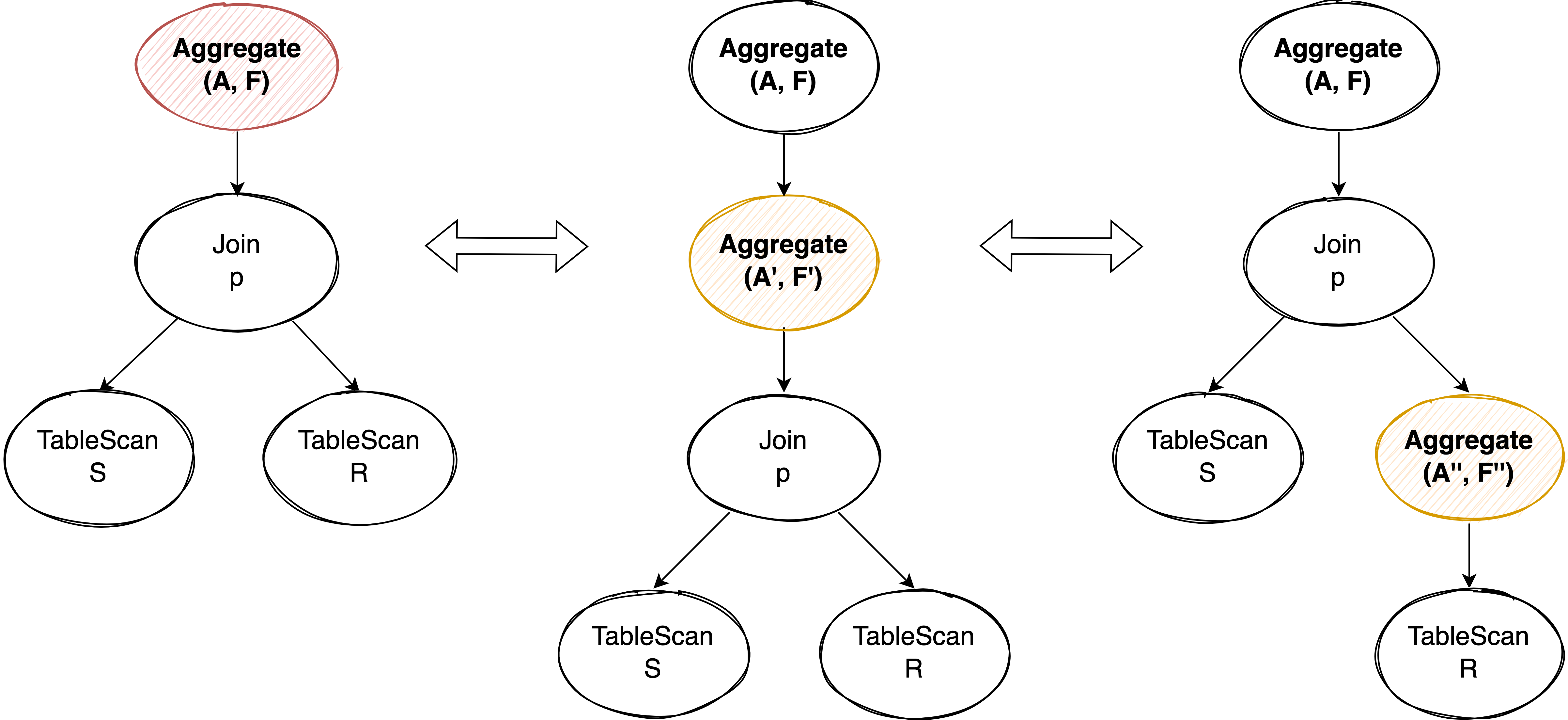
Local Aggregate

理论上来说，任何 Aggregate 都可以拆成 Local Aggregate + Global Aggregate 两阶段聚合的形式。当我们不能完全把 Aggregate 下推到 Join 下面时，适当的拆分 Local Aggregae 使 Local Aggregate 下推到 Join 下面，可以减少 Join 的数据量提升整体执行性能。

Local Aggregate 有一个很好的性质：它的 group by column 可以在原来 Global Aggregate 的基础上随意扩充，因为扩充 group by column 仅仅是进一步划分 Global Aggregate 一个 group 数据的子集，对最终的 Global Aggregae 来说不会产生正确性影响。我们可以利用这个特点来构造满足下推条件的 Local Aggregate：

  1. 将 join condition 中使用的 R 表上的 column 添加到 Local Aggregate 的 group by column 中，使得 join condition 代表的 Filter 作用在 Local Aggregate 的 group 上。
  2. 对于 Global Aggregate 中的聚合函数，如果它使用了左表数据，可以把该聚合函数在 Local Aggregate 中改写成 count(*)，并在 Local Aggregate 后增加一个 Project 和 count(*) 的结果一起计算模拟出曾经 Global Aggregate 需要的 Local Aggregate 结果，比如 sum(s.a) 可以改写成 s.a*count(*)。

SegementApply #

什么是 SegmentApply #

Segmented Apply 可以看做是一种 partitioned nested loop join。它将左表的数据按照指定的 column 先进行 partition，然后把每个 partition，也就是论文中说的 segment，作为输入交给右表，完成关联子查询的计算，最后返回这一个 partition 对应的结果。

在关联子查询去关联后，经常发生两个几乎一样的 sub plan join 到一起的情况，比如 TPC-H Q17 去关联后的等价 SQL 如下，lineitem 表和 lineitem 表上的聚合结果发生了一次 join：

TPC-H Q17

从语义上来说，这个 join 是希望对 lineitem 表按照 l_partkey 分组，求出每组的 l_quantity 平均值，并输出低于平均值的 20% 的所有 lineitem 数据。用 SegmentApply 可以描述成下图所示的执行计划：

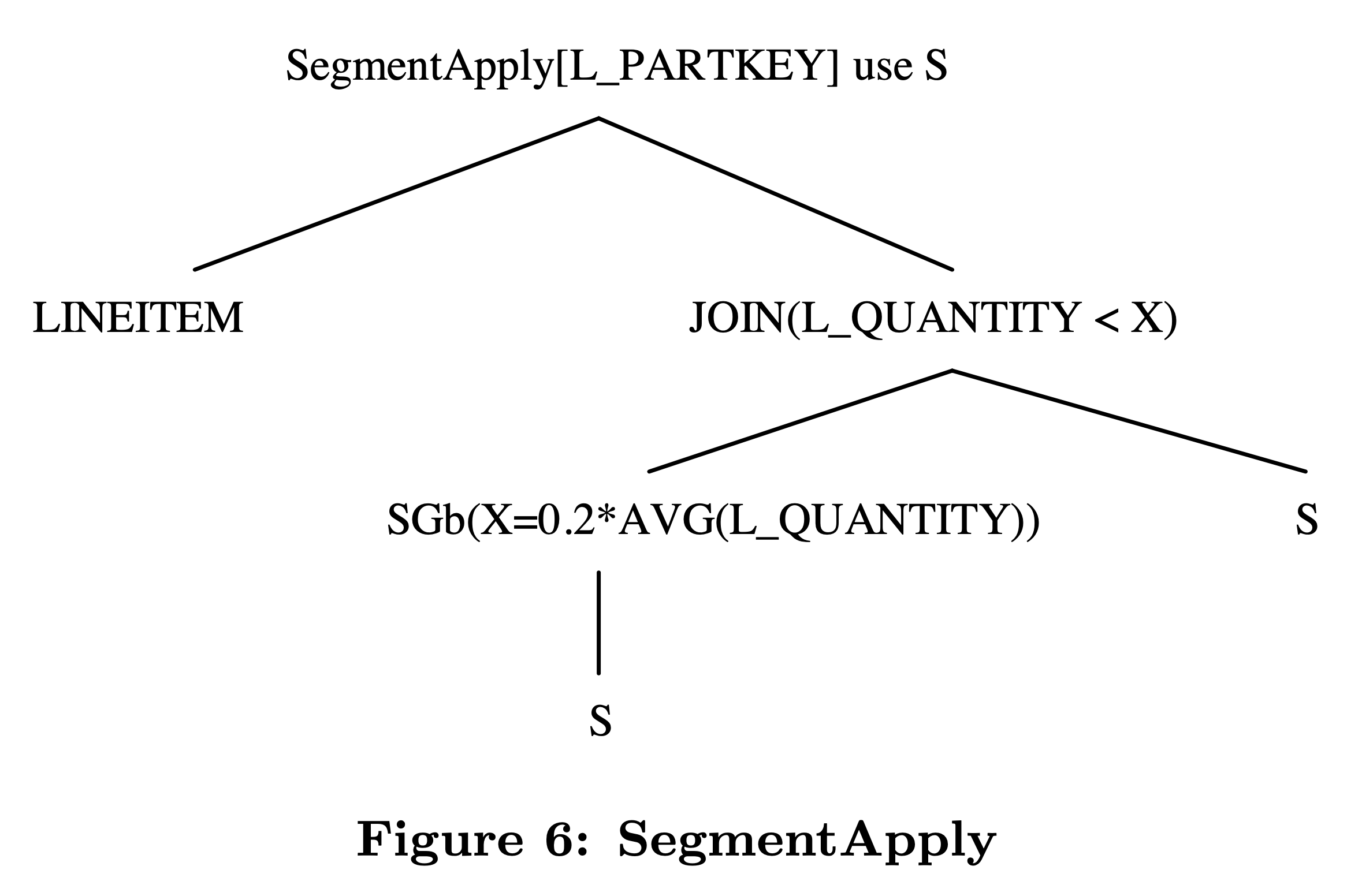
Segment Apply

Transform Join to SegmentApply #

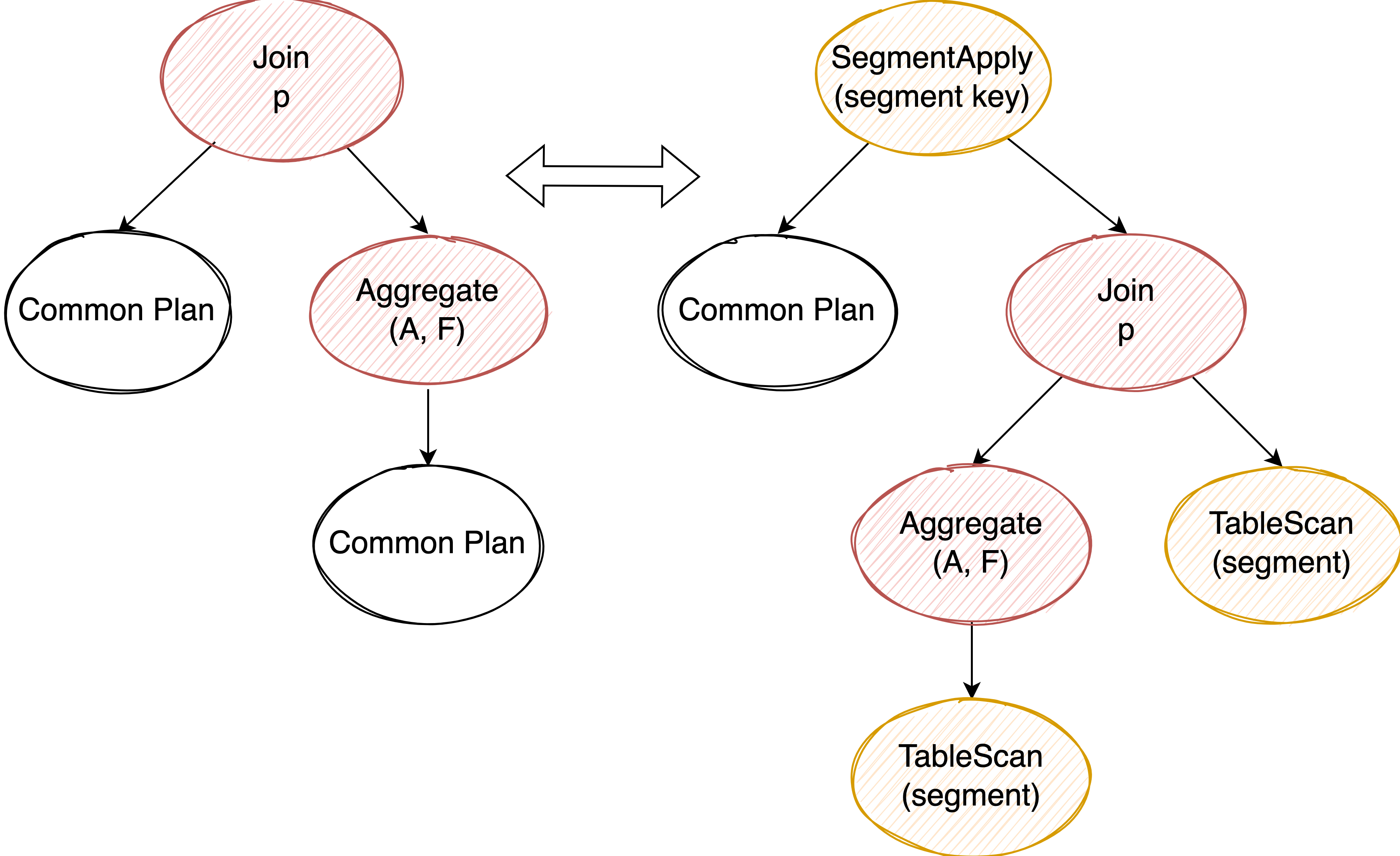
Transform to Segment Apply

观察 join condition，看是否是两个来自相同 table 或 sub plan 的相同 column 在做等值比较，找到这样的 pattern 后，这些 column 就可以用来作为 common sub plan 的 segment key。

个人理解：判断 join condition 两个 column 是否是同一个 column 可以用 column 的血缘分析来解决。当 join 确定后，common sub plan 也确定了，比较粗糙的做法是直接认定 join 的左子树为 common sub plan ，然后看右孩子是否是 aggregate，以及这个 aggregate 的子树是否和 join 的左子树相等。

Moving SegmentApply Around Joins #

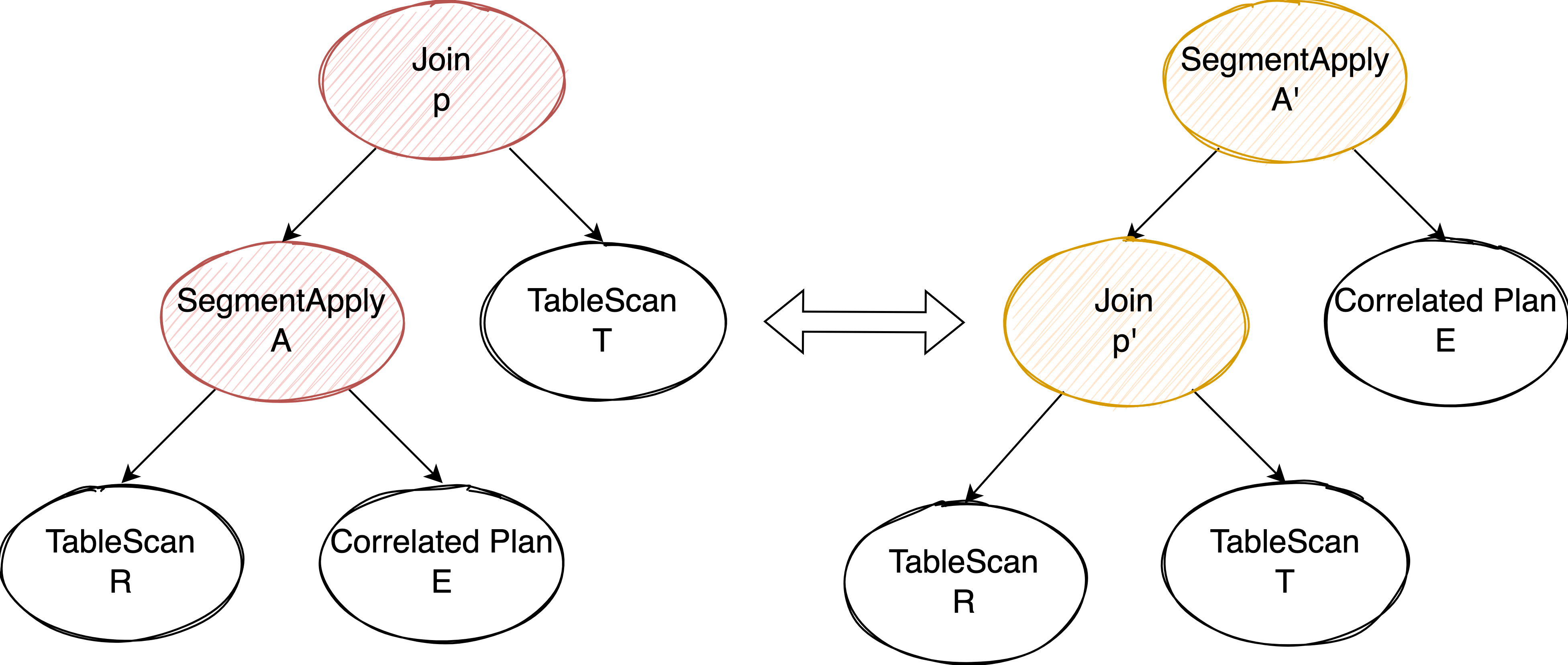
Move SegmentApply Around Join

回到上面 TPC-H Q17 的例子，如果我们能够先执行 lineitem 和 part 表的 join 再进行 SegmentApply，说不定 Join 能够裁剪一部分 lineitem 表的数据，使得后续的 SegmentApply 能够轻松一些，提升整体执行效率。这就要求我们能够变换 SegmentApply 和 Join 的执行顺序。

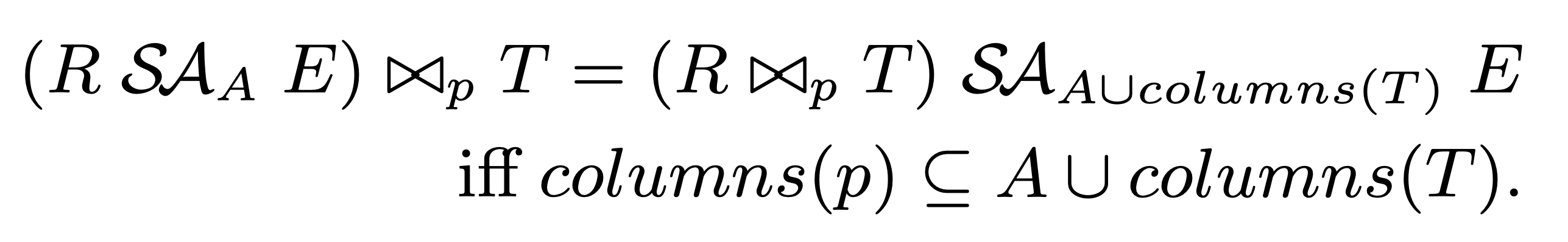
formal Transformation Rule

要将 Join push down 到 SegmentApply 的左孩子下面，当且仅当 Join 中使用的 column 是 SegmentApply 的 segment key 和 T 表某个主键或唯一索引的 column 子集：

  1. Join 可以看做是 Cross Join + Filter，我们要求下推前后 Join Filter 的效果保持一致，那么就需要这个 Join Filter 是作用在 segment 这个粒度上的，因此也就要求 Join Filter 使用的 column 是 segment key 的子集（满足 functional dependency）
  2. 如果 Join 中使用了其他 Filter 也有办法绕过，因为 Join 是 Cross Join + Filter，那么可以再单独提取一个 Filter 保留在原地，把不满足下推条件的 Join Condition 保留在这个 Filter 中
  3. 对于一行 R 表 match 多行 T 表的情况，如果 T 表有主键或唯一索引，我们就可以建立起主键或唯一索引到每一行数据的 functional dependency 关系，并且因为 Join 的 Filter 也是作用在 R 表的 segment key 和 T 表的这个主键或唯一索引上，我们可以认为 Join 的 Filter 是对 R 表的 segment key + T 表的主键所指向的更细粒度的 segment 进行过滤。因此 Join 下推后，这个 T 表的主键和唯一索引也需要作为 segment key 补充到新的 SegmentApply 上去，保证和原来执行计划的语义一致性。

经过这个优化，以及在 SegmentApply 中消除掉等价的 column 后，TPC-H Q17 的执行计划就变成了下图所示：

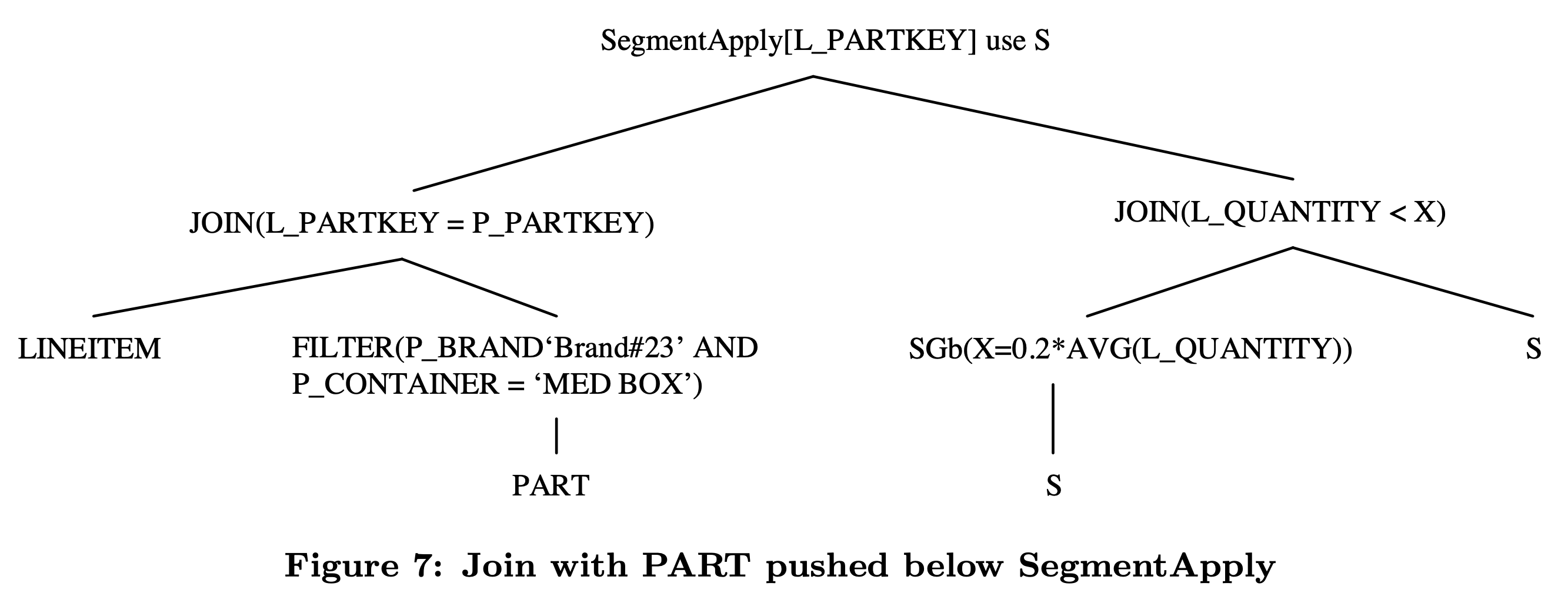
Q17 Final Plan

总结 #

以上就是这篇论文的主体内容，论文还在 2.4 和 2.5 小结介绍了其他几种子查询的类型，比如当子查询出现在 SELECT 列表中时，为了确保 scalar function 的语义引入了 Max1Row 算子，感兴趣的朋友们可以去读一读原文，我们不在文章中继续展开了。

将子查询改写成 Apply、SegmentApply 等算子使我们可以应付绝大多数场景的子查询问题，论文提出的各种优化规则将子查询优化的问题分治成了一个个小问题，也让代码实现和维护变的更加简单，非常值得学习。