[VLDB 2006] Analysis of Two Existing and One New Dynamic Programming Algorithm for the Generation of Optimal Bushy Join Trees without Cross Products
Table of Contents

天堂湖,乌孙古道,2023
INTRODUCTION #
《 Analysis of Two Existing and One New Dynamic Programming Algorithm for the Generation of Optimal Bushy Join Trees without Cross Products》这篇论文先分析了 DPsize 和 DPsub 这两个常用的 join reorder DP 算法,发现它们在枚举 DP 使用的 csg-cmp-pair 时并不高效,实际时间复杂度远高于理论下界。作者提出了一种高效的 csg-cmp-pair 的枚举算法和 DPccp 算法,使得每个 csg-cmp-pair 仅被枚举一次,在各种类型的 join graph 和 join size 下都能表现出良好的 DP 性能。
Guido Moerkotte 和 Thomas Neumann 后面基于 DPccp 和 hyper graph 提出了新的 DPhyp 算法,这篇论文对理解 DPhyp 算法也有一定帮助。
ALGORITHMS AND ANALYSIS #
在讲 DPccp 之前,先看看 DPsize 和 DPsub 这两个常用的 join reorder 算法,它们都能寻找到不包含 cross-product 的最优 bushy tree,只是时间复杂度不同。
DPsize: Size-Driven Enumeration #
在著名的《 Access Path Selection in a Relational Database Management System》一文中,Selinger 提出了一种自下而上的 join reorder DP 算法。该算法按照连接节点数量从小到大的顺序为每个 interesting order 计算出了最佳的左深树 join order。虽然 Selinger 的 join reorder 算法只考虑了左深树,但是可以在这个算法思路的基础上扩展出能够枚举 bushy tree 的 DPsize 算法,其伪代码如下所示:

DPsize 的思路简单直接:将 n 个表的 join order 问题分解成 k 和 n-k 个表的子问题。包含 1 个表的最佳 join order 就是该表本身,这是 DP 的初始解。然后从小大到大计算每个 join size 下的最佳 join order。在计算包含 s 个表的 join order 时,通过枚举所有 s1+s2=s 的 s1 和 s2 各自的最佳 join order 来确定包含 s 个表的最佳 join order。
注意代码中的两个 counter。一个是 InnerCounter,它描述了该算法的时间复杂度,一个是 CsgCmpPairCounter,它描述了该算法枚举的所有联通的、有效的 csg-cmp-pair (S1, S2) 的数量。后面 DPsub 也统计了同样的 counter,便于对比分析。
作者总结了 chain、cycle、star 和 clique 这 4 种 join graph 上的 InnerCounter 计算公式如下:
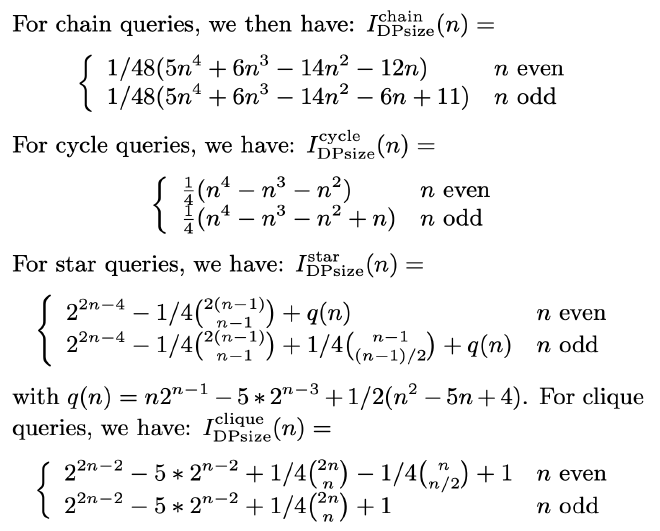
DPsub: Subset-Driven Enumeration #
DPsub 起源于 Vance 和 Maier 在《 Rapid Bushy Join-order Optimization with Cartesian Products》这篇论文提出的 join reorder 算法。原算法考虑了 cross-product,但因为 cross-product 极大的增加了 join order 的搜索空间,作者将其修改为不考虑 cross-product,得到了下面 DPsub 的伪代码:

DPsub 是一种状态压缩 DP。它利用一个整数的各个比特位来表示有哪些表参与 join(第 i 位为 0 或 1 分别代表第 i 个表是否参与 join)。熟悉状态压缩 DP 和位运算的朋友们应该比较容易理解这个算法。
每个整数 i 都代表了一个节点子集,也就是一个 DP 状态。状态 i 代表的点集用 S 表示,只对那些联通的点集 S 计算最佳 join order。在计算时依次枚举 S 的所有子集 S1 和对应的补集 S2=S\S1,根据他们的最佳 join order 得到点集 S 的最佳 join order。
从 1 到 2^n-1 递增的枚举所有可能的 DP 状态,这样的枚举方式可以保证在计算状态 i 的最优解时,i 的所有子状态已经在之前的枚举过程中计算出来了,状态 i 的最优解可以根据这些最优子状态计算出来。
同样的,作者总结了 chain、cycle、star 和 clique 这 4 种 join graph 上的 InnerCounter 计算公式如下:
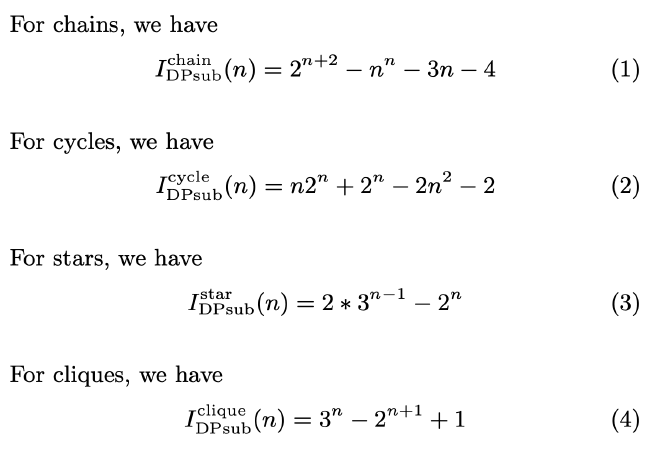
Algorithm-Independent Results #
csg-cmp-pair:csg 是 connected subgraph 的缩写,cmp 是 complement 的缩写,如果 S1 和 S2 是两个不相交的联通子图,并且在 S1 中的某个节点 v1 和 S2 中的某个节点 v2 有一条边(也就是 join predicate),那么就说 (S1, S2) 是一个 csg-cmp-pair。另外子图和补图关系是相互的,(S2, S1) 也是一个 csg-cmp-pair。把 query graph 中 csg-cmp-pair 的个数用 #ccp 表示。#ccp 有一些非常重要的性质:
- 它是 query graph 的固有属性,和具体的 join reorder 算法无关,query graph 决定了 #ccp
- 它是所有正确的 join reorder 算法中 CreateJoinTree 调用次数的下界,也就是 join reorder 算法的时间复杂度下界。
作者总结了 DPsize、DPsub 在 chain、cycle、star、clique 这 4 种 join graph 上的 #csg 和 #ccp 的计算公式,这些公式表明了 join reorder 算法的时间复杂度下界:

Sample Numbers #
作者抽样计算了几个 join size 下,DPsize、DPsub 算法中 InnerCounter 以及 #ccp 的数值,如下表所示:
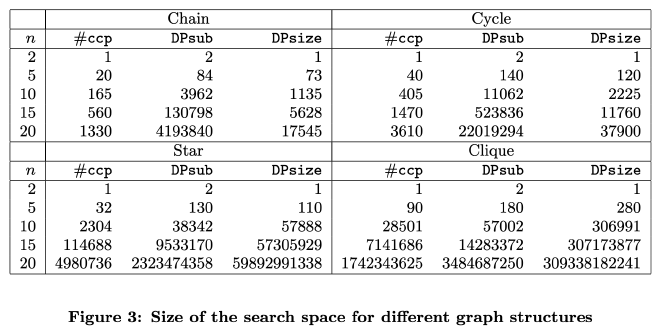
可以看到:DPsub 和 DPsize 在 chain、cycle、star、clique 类型的 query graph 中各有优劣,一个最大的特点是,不管 DPsize 还是 DPsub,它们的 InnerCounter 都远高于 #ccp,代表它们在枚举 csg-cmp-pair 时有许多失败尝试,距离 DP 算法的理论复杂度下界 #ccp 有好几个数量级的差距。因此作者就想设计一种能够达到 #ccp 这个理论时间复杂度下界的 DP 算法,也就是后面将要介绍的 DPccp。
THE NEW ALGORITHM DPCCP #
作者在这个章节详细介绍了能够快速且不重复的枚举所有 csg-cmp-pair 的 DPccp 算法,并利用图论和数学证明方法证明了这个枚举算法的正确性。
Problem Statement #
因为要解决的是 DPsize 和 DPsub 这两个 join reorder 算法枚举了大量不联通的子图的问题,因此 DPccp 的目标就变成了如何高效的枚举所有联通的 csg-cmp-pair 一次且仅一次,以达到 DP 算法理论时间复杂度的下界 #ccp,同时也有一些限制条件:
- csg-cmp-pair 的枚举顺序需要能够用来进行 DP,也就是当枚举到 (S1, S2) 这样的 csg-cmp-pair 时,S1 和 S2 各自所有的 csg-cmp-pair 都已经枚举过了。
- 另外是生成 csg-cmp-pair 的开销需要是常数级别,或者至少是线性级别,这样才能在时间复杂度上优于 DPsize 或 DPsub。
DPccp 的伪代码如下所示,通过枚举所有的 csg-cmp-pair,逐步求解最优 join order:

Enumerating Connected Subsets #
要枚举 csg-cmp-pair,我们可以考虑如何枚举所有的 csg。先来看看如下定义:
- neighborhood N(v):所有和节点 v 有一条边相连的点集
- neighborhood N(S):所有和点集 S 中的节点有一条边相连且不在 S 中的点集
一种利用 neighborhood 来枚举 csg 的方法是:从一个 csg S 出发,先寻找它的 neighborhood N(S),然后枚举 N(S) 的子集并和 S 组成新的 csg S’,然后递归的调用这个函数来枚举所有从 S’ 出发的 csg。不过这样的问题是一些 csg 可能被重复枚举。
要解决重复枚举的问题,作者先用 BFS 方式遍历每个节点并给出一个递增的编号,然后按照节点编号从大到小逆序枚举所有的出发节点,并从这些出发节点开始枚举所有的 csg:
- 从节点 vi 出发枚举 csg 时,不考虑那些编号比 i 小的节点 vj,因为这些节点会在后面被遍历到
- 从 csg S∪S’ 出发枚举 csg 时,不再考虑 N(S),因为这些节点也会在后面枚举的新的 S’ 遍历到
枚举所有 csg 的伪代码如下所示,入口函数是 EnumerateCsg,辅助函数是 EnumerateCsgRec,Rec 应该是 recursive 的意思,隐含着该函数会不断被递归调用的信息:

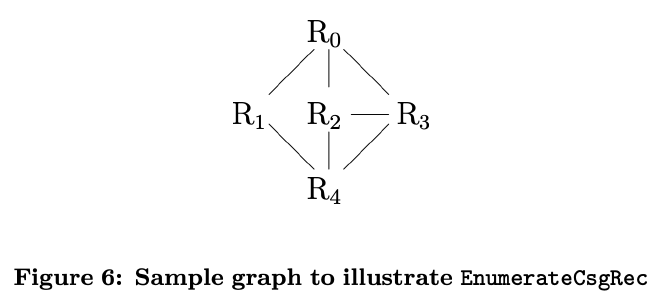
下面的例子展示了该算法的执行过程,这是一个 5 节点的 join graph,已经按照 BFS 的方式从 R0 出发对节点进行编号,跟着例子走一遍可以更深刻的体会这个枚举过程:
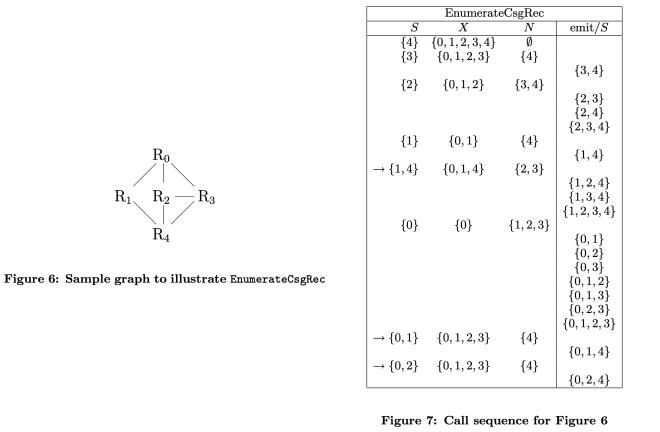
Enumerating Complements of Connected Subgraphs #
上面的 EnumerateCsgRec 也可以用来继续枚举所有和 csg S1 联通的补图 S2:
- S2 一定包含 S1 的 neighborhood N(S1) 中的某些节点
- 仅枚举所有 min(S1) < min(S2) 的 csg-cmp-pair,其中 min(S) 指的是 S 中最小的节点编号
EnumerateCmp 的伪代码如下所示,其中 Bi(N) 指的是点集 N 中所有编号小于等于 i 的点集。为了枚举所有 min(S2) > min(S1),且和 S1 没有任何交集的 csg S2,需要将所有编号小于等于 min(S1) 以及 S1 中的节点都排除掉,将这些排除掉的节点初始化 X 中。
然后按照节点编号从大到小遍历 S1 的 neighborhood N(S1)\X 后的点集 N,从 N 中每个节点出发构造和 S1 相连的 csg。同样的,为了避免重复枚举 S2,每次枚举的 min(S2) 也都确保比后续要枚举的 min(S2’) 要大,所以在调用 EnumerateCsgRec 时需要把 Bi(N) 也加到 X 中去。

还是以这个 5 节点的 join graph 为例,如果 S1={R1},那么初始化的 X={R0, R1},它的 N={R4},构造出的第一个 cmp 就是 {R4},接着调用 EnumerateCsgRec(G, {R4}, {R0, R1}∪{R4}) 可以得到 {R4, R2}, {R4, R3}, {R4, R2, R3},这 4 个 cmp 和 S1 共同构成了用于 DP 的 4 个 csg-cmp-pair:
Correctness Proof #
整个 DPccp 算法的正确性是由这个 csg-cmp-pair 枚举算法的正确性来保证的,作者在这一章节花了比较长的篇幅严谨的证明了 csg-cmp-pair 枚举算法的正确性,篇幅所限这里不再展开,感兴趣的朋友可以阅读原文。
EVALUATION #
作者实现和测试了 DPsize、DPsub 以及新提出的 DPccp 这 3 种 DP 算法在 chain、cycle、star 以及 clique 这 4 种 join graph 下不同 join size 的时间开销,以 DPccp 的时间为基准和 DPsize、DPsub 的时间进行了对比:
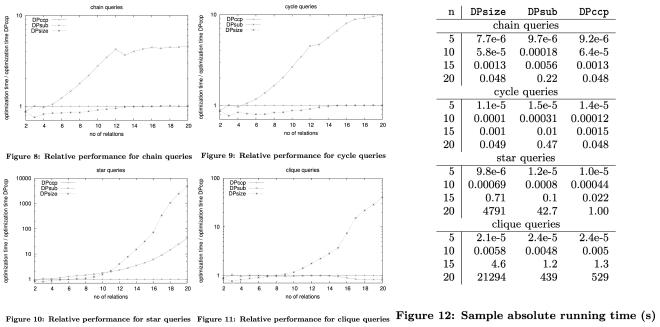
综合来看 DPccp 在各种 join graph 以及各种 join size 情况下性能表现都很不错,是个非常不错的 join order DP 算法。